4730. Fibonacci
Fibonacci numbers is a sequence of numbers f(n), defined by the formula:
·
f(0) = 1,
·
f(1) = 1,
·
f(n) = f(n – 1) + f(n – 2)
Given a value of n, find the n-th Fibonacci number.
Input. One nonnegative
integer n (n ≤ 45), representing the Fibonacci number to be printed.
Output. Print the n-th Fibonacci
number.
|
Sample
input |
Sample
output |
|
4 |
5 |
SOLUTION
Fibonacci numbers
Algorithm analysis
Compute all Fibonacci
numbers and
store them in the fib array by assigning fib[i]
= f(i). Then print the desired Fibonacci number.
Example
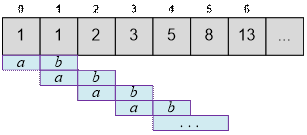
The fib
array will be filled as follows:

Algorithm implementation
Compute the Fibonacci
numbers and
store them in the fib array: fib[i] = f(i).
#define MAX 46
int fib[MAX];
Fill the fib array according to the recursive formula.
fib[0] = 1;
fib[1] = 1;
for(int
i = 2; i < MAX; i++)
fib[i] = fib[i-1] + fib[i-2];
Read the input value of n. Print the
answer.
scanf("%d",&n);
printf("%d\n",fib[n]);
Algorithm implementation – recursion
Declare the fib array to store
Fibonacci numbers: fib[i] = f(i).
#define MAX 46
int fib[MAX];
The recursive function f computes
the n-th Fibonacci number. The memoization technique is used.
int f(int
n)
{
if (n <=
1) return 1;
if (fib[n] !=
-1) return fib[n];
return fib[n]
= f(n-1) + f(n - 2);
}
The main part of the program. Read
the value of n.
scanf("%d",&n);
Assign the value of -1 to all elements of fib
array.
memset(fib,-1,sizeof(fib));
Compute and print the value f(n).
printf("%d\n",f(n));
Algorithm implementation – iteration
Read
the input number n.
scanf("%d", &n);
Handle
the base case.
if (n == 0 || n == 1)
{
printf("1\n");
return 0;
}
Let
us assign:
·
the 0-th Fibonacci number to the variable a;
·
the 1-st Fibonacci number to the variable b;
Initially, the variables a and b contain
two consecutive Fibonacci numbers.
a = b = 1;
for (i = 2; i <= n; i++)
{
The variables a and b contain two
consecutive Fibonacci numbers.
a = f(i
– 2),
b = f(i
– 1)
Compute the next Fibonacci number:
c = a
+ b = f(i – 2) + f(i
– 1) = f(i)
c = a + b;
Perform a shift, as a result of which a = f(i – 1) and b = f(i).
a = b;
b = c;
}
Print
the answer. The variable b contains the value of f(n).
printf("%lld\n", b);
Java implementation
import java.util.*;
public class Main
{
public static int MAX =
46;
static int fib[] = new int[MAX];
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
fib[0] =
1; fib[1] = 1;
for(int i = 2;
i < MAX; i++)
fib[i] = fib[i-1] +
fib[i-2];
System.out.println(fib[n]);
con.close();
}
}
Java implementation – constant memory
import java.util.*;
public class Main
{
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int a = 1,
b = 1, temp;
for(int i = 0;
i < n; i++)
{
temp = a;
a = b;
b = temp + b;
}
System.out.println(a);
con.close();
}
}
Java implementation – recursion, TLE
import java.util.*;
public class Main
{
static int f(int n)
{
if (n <= 1) return 1;
return f(n-1) + f(n - 2);
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
System.out.println(f(n));
con.close();
}
}
Java implementation – recursion with
memoization
import java.util.*;
public class Main
{
static int fib[] = new int[46];
static int f(int n)
{
if (n <= 1) return 1;
if (fib[n] != -1) return fib[n];
return fib[n] = f(n-1) + f(n - 2);
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
Arrays.fill(fib, -1);
System.out.println(f(n));
con.close();
}
}
Python
implementation – list
To store Fibonacci
numbers,
declare a list fib: fib[i]
= f(i).
fib = [1,1]
Fill the fib array according to the recursive formula.
for i in range(2,46):
fib.append(fib[i-1] + fib[i-2])
The
main part of the program. Read the value of n.
n = int(input())
Compute and
print the value f(n).
print(fib[n])
Python
implementation –
constant memory
n = int(input())
a, b = 1, 1
for i in
range(n):
a, b = b, a + b
print(a)
Python
implementation – memoization
To store Fibonacci
numbers,
declare a list fib: fib[i]
= f(i).
fib = [-1] * 46
The
recursive function f computes the n-th Fibonacci number. The memoization technique is used.
def f(n):
if n <= 1: return 1
if fib[n] != -1: return fib[n]
fib[n] = f(n - 1) + f(n
- 2)
return fib[n]
The
main part of the program. Read the value of n.
n = int(input())
Compute and
print the value f(n).
print(f(n))